Nanoestructuras desordenadas

Investigación Miembros del Grupo Publicaciones regresar Nonlinear model q = 53.13^o, Molybdenum Experiment Nonlinear model q = 20.4^o, ZnO Experiment

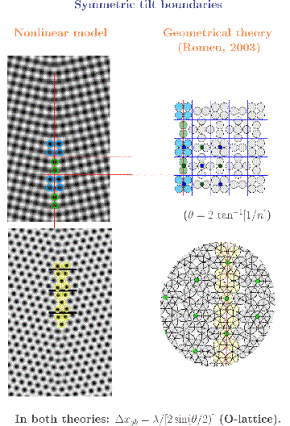
Investigación Universality of defects in periodic phases: nonlinear models of pattern formation, quasi crystals and real solids. Grain boundaries form when two monocrystals of different orientations meet and compete for filling space in a limited region of space, a common situation in materials. These objects are particularly difficult to study theoretically. We wish compare the results given by two independent theories, that allow a systematic description of the geometry of grain boundaries at the microscopic scale. These theories are based on a priori very distinct backgrounds and borrow ideas from two fields of physics apparently unrelated: nonlinear pattern formation and quasi-crystals. The first approach is directly based on the weakly nonlinear analysis of Swift-Hohenberg-like models for pattern forming systems. The second approach is essentially geometrical and starts from the idea that any grain boundary is a particular kind of quasi-crystal. For the examples presented here (symmetric tilt boundaries in two-dimensional crystals), both methods predict quantitatively the same structures, independently of any tunning parameter. Our results suggest a kind of universality of frustration and competition effects near a defect in crystalline arrangements. Some applications to nanograins will be considered. Investigadores Denis Boyer (IFUNAM) David Romeu (IFUNAM) Estudiantes Publicaciones regresar