

Abstract
Groups of Nasutitermes cf. aquilinus termites of different sizes were studied under resource-deprived conditions to investigate the relationship between increasing group size and individual longevity. It was found that survival was significantly lower for isolated individuals and higher for individuals in bigger group sizes, suggesting that survival is strongly enhanced by social interactions only. A computer model, incorporating individual interactions among mobile automata, can plausibly help to provide further insights into this phenomenon.
Introduction
Interactions among the many individuals that compose social groups, generate a range of behaviours not present at the individual scale. Spatio-temporal patterns of collective behaviour develop following the concurrent activity of individuals that do not have pre-programmed information for generating these. Hence, such patterns are not observed when individuals are in isolation (Oster & Wilson 1978). Social facilitation has been regarded as one of the most basic manifestations of such phenomenon and is commonly defined as the ordinary patterns of behaviour that are initiated or increased in pace or frequency by the presence or actions of another animal (Wilson, 1980). Social facilitation is then a synergetic process, or more precisely, a non-linear response behaviour whose prerequisite is the capacity of an animal to sense, excite and communicate with others.
Social facilitation has been found in many invertebrate species (e.g. Kurta, 1982; Hosey et al., 1985; El Bakary & Fuzeau-Braesch, 1987) and occurs ubiquitously among the social insects. It has been studied in wasps (Parrish & Fowler, 1983; Fowler, 1992), bees (Grassé & Chauvin, 1944; Chauvin et al., 1985), ants (e.g. Chen 1937; Chauvin, 1944; Grassé & Chauvin, 1944; Lamon & Topoff, 1985; Klotz, 1986; Salzemann & Plateaux, 1988; Hölldobler & Wilson, 1991) and termites (e.g. Grassé & Chauvin, 1944; Grassé, 1946; Lenz & Williams, 1980; Williams et al., 1980; Afzal, 1983; Okot-Kotber, 1983; Springhetti, 1990).
Most of the classical studies of social facilitation focus on task performance by isolated individuals contrasted with that of individuals in groups. In termites, however, studies of a different nature have been carried out, investigating survival as a function of group size. Williams et al. (1980) considered 3 species of Cryptotermes and investigated the survivorship for groups of 1, 2, 4, 8, 16 and 32 pseudoworkers kept with food supply. They found that survival was much lower in termites kept individually than in those in groups of 2 and, similarly, it was lower in groups of 2 than in groups of 4 or 8 and so on. A different approach was adopted by Lenz & Williams (1980) who investigated the survival of Nasutitermes nigriceps (Hald) in environments rich in food, but with different container sizes and found that survival and wood consumption decreased with increasing container size. This experiment provided strong evidence that interactions between social individuals are crucial to survival, since increasing the container size is equivalent to a reduction of the group density and hence of the rate of contacts and interactions. In these two experiments, however, Cryptotermes and Nasutitermes were provided with food sources, making the possibility of explaining longevity only as a function of social interactions far from straightforward. Grassé (1986) commented on such a correlation between group size and longevity in termites, but it is not clear whether his experiments were carried out with or without food supply (he stated that the termites were kept in optimal conditions, which suggests that food was available).
In this article, we provide experimental evidence that the survival of groups of Nasutitermes cf. aquilinus termites in resource-deprived environments is significantly correlated with the group size and therefore with the rate of social interactions. We also describe a computer-simulated model of social interactions to show how interactions between mobile automata increase the individual longevity and hence that of the group.
Materials and methods
Nasutitermes cf. aquilinus workers (third instar and beyond) were collected from a single wild colony from Viçosa, Minas Gerais in Brazil and were randomly placed in groups of 1, 2, 4, 8 and 16 individuals (four replicates). The groups were confined in test tubes made of transparent glass (9.5 cm x 1.4 cm) with hermetically sealing rubber caps. The tubes were kept horizontally separated by plastic foam to prevent stridulation or other mechanically transmitted signals to propagate between the tubes. The workers were allowed to acclimatise for 12 hours and were incubated in the dark at 25o C 0.5. No food or water was provided. The samples were kept in darkness and were exposed to light during the counting of survivors only (no more than five minutes).
Observations were made at 12 hours intervals. The experiment was continued until 24 hours after all the solitary individuals were dead in order to check the consistency of the trend observed in the multi-individual treatments. Seven observations were made. The data were subjected to survival analysis, using Weibull frequency distribution, as described by Crawley (1993) (see also Pinder III et al. 1978). Significance was assessed by deleting terms from a model until a change of deviance with a p<0.001 was observed. Differences between treatments were evaluated by aggregating factor levels until the consequential change in deviance was significant at p<0.001.
Results
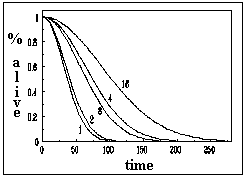
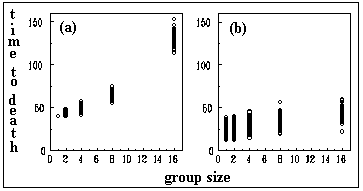
All individuals were alive at the time of the first observation and the first dead workers began to appear 24 hours after being confined. The analyses of the mortality figures for the seven observations give significant results that allow us to conclude that mortality was higher for isolated workers and lower for individuals in groups (c2 = 25.44; 4 d.f.; p < 0.001). A tendency that is easily identified in the data plotted in Figure 1. It was clea from the observations, that workers in groups tended to cluster together and to engage in social interactions that included antennations and grooming and that this behaviour was more conspicuous in larger groups.
Modelling
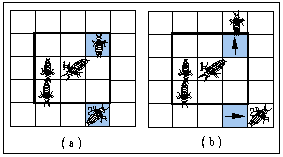
In order to simulate the process of increased longevity, we developed a computer model of the type known as individual-based or mobile cellular automata (Miramontes et al. 1993a; 1993b; Solé et al. 1993a; 1993b). In our model, a set of interacting individual agents (termites in this case) are defined over a rectangular grid and follow some of the simple behavioural rules observed in real termites (Figure 2). Each cell of the grid is occupied by only one individual and termites are able to move randomly to empty adjacent cells, where they interact with those in the eight most immediate cells (reflecting the fact that real termites interact mainly by direct body contact: antennations, grooming and trophallaxis).
We define a state variable (a) for each individual termite indicating, whether the individual is dead or not. A termite is considered to be alive while this variable is greater than zero and dead otherwise. This variable increases each time a termite interacts with others, reflecting the ability of termites to excite and respond to the presence of colony mates. This quantity (a) inevitably declines to zero after a finite time because termites in isolation do not have access to external inputs.
The process of social interactions is defined through a coupling function that reflects the fact that, firstly, individual termites cannot be infinitely excited after repeated interactions, thus the function has to be bounded (sigmoidal in shape) and, secondly, the activity of an individual will increase or decrease according to parameters representing the degree of excitability. A function that accommodates these requirements and is widely used in models of excitable media (typical for neural networks) is the hyperbolic tangent function. Hence, the coupling between interacting termites is defined as follows:
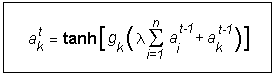
where ait is the activity of the i-th termite (maximum of eight) in the first neighbourhood of the ak termite at time t. gk is the individual excitability parameter and l is a parameter measuring the group-level ability to communicate. The simplicity of the model does relies on only two parameters that are biologically justifiable.
The parameter gk (often called the gain of the hyperbolic tangent function) reflects interindividual differences in the capacity for excitation and interaction (i.e., some individuals are more likely to respond to stimuli of the same intensity than others). It is well-known that young adults, in many social species, respond to antennations from nestmates more readily than older ones, a fact that has been quantified in the case of the spontaneous activations of ants in the genus Leptothorax (Cole, 1992). Individuals may respond to their mates and behave in different ways depending on their state of health. Parasitised termites, for example, suffer profound morphological modifications (Krishna & Weesner, 1970; Grassé, 1986; ) that are likely to provoke changes in their behaviour. An extreme example of this is observed in parasitised bumblebees which may even desert the colony, stopping all forms of interaction with their nestmates (Poulin, 1992; Müller & Schmid-Hempel, 1992). Hence, young or healthy individuals are characterised by high values of gk , while old or unhealthy individuals would have a lower value.
As previously said, the second parameter (l) quantifies the group-level ability to communicate and is equal for each individual. This parameter indicates the strength or intensity with which the members of a given species interact among themselves. A group of non-social individuals, that do not interact at all, would have a l of zero, that is, a collection of non-cooperative selfish individuals. Organisms characterised by a high value of l would be the most socially developed, while those characterised by medium values would be the species of lower degree of sociability (gregarious and presocial species).
Simulations were started by estimating the values of the lattice size that would give the correct termite group density. The values of gk and l also need to be estimated as well. Lattice size was found by measuring the average worker area (the projected polygon formed by legs and antenna). This area was approximately 18.3 mm2 . The effective walking area inside the test tubes was 760mm2. Therefore, about 42 individuals would saturate this space giving a lattice size of 67 = 42 cells.
In order to estimate gk , we assumed only one individual in the lattice, so that the coupling function reduces to :

that is clearly independent of l. Since gk determines the individual time-to-death, it is possible to estimate the average time-to-death from the four experiments with groups of size one and then find an average value that gives the same average time-to-death in the model. The average time-to-death was 42.0 hours in the experiment and 42 time steps in the computer simulation, using . The initial value of the state variable was set to 1.0.
The parameter l was estimated by noting that the average time-to-death in the groups of 16 termites was 123 hours. We found that given , a l of 0.3 gave a time-to-death of 123 time steps in automata groups of size 16. It is important to remember that since time in the experiment and time in the model are only roughly equivalent, the parameter values estimated are just good approximations that permit similar qualitative behaviour between the experiment and the simulation. In fact, we found that, when using other values of these parameters, the qualitative behaviour of the model was quite robust.
As mentioned before, inter-individual variability must introduce important constraints to the way a society of insects organise and work. Oster & Wilson (1978) argued that individual size (S), age distribution (A) and caste composition (C) are three factors that critically regulate the ergonomic efficiency of the whole society in such a way that the demography may even be of an adaptive nature. It seems reasonable then to assume that the success of an insect society highly depends on the behavioural diversity of its individual components. The introduction of demographic factors (S, A and C) seems then to be a very interesting field to investigate and we used our model to perform an exercise in this direction.
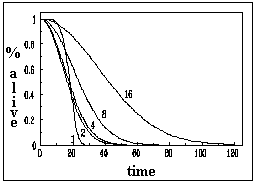
Inter-individual variability was tested by comparing the performance of groups of different sizes depending on whether the value of gk was the same or different for all individuals. The results are shown in figures 3a and 3b. In the case where gk had a constant value (0.7), we observed that social facilitation was quite evident. Groups of 16 individuals clearly survived more than groups of smaller size and the individual automata in those groups survived about 4 times longer on average, than isolated automata (see figure 4). A second simulation was carried out where the individual values where randomly generated on an interval with a flat probability distribution (gk = 0.5 0.2), so that there were individuals with high (0.7 maximum), medium and low (0.3 minimum) values of gk intermixed. This scenario is shown in figure 3b where some results are evident. First, while social facilitation is still present, it is of a less intense nature. This is explained by the fact that individuals with low gk , as said before, are not particularly good at interacting and participating in the generation of collective properties. This would be the fraction of very old or unhealthy individuals that, in natural insect societies, are sometimes eliminated, relegated or isolated from the normal colony life. It is tempting to argue that the elimination of individuals, with impaired abilities for interaction, may be in order to avoid a decrease in the average ergonomic efficiency of the colony (the same may apply to the parasitised bumblebees that self-defect). A second result derived from contrasting figure 3a against figure 3b is that inter-individual variability does not change the variance of the time-to-death when groups size is large. This means that social interactions may partially homogenise the efficiency of the social tasks, regardless of the fact that insect societies are formed by individuals with high variability in individual performance.
It would be highly desirable to have experiments that provide exact demographic parameters so that the values of gk could be arranged accordingly in such a way as to test whether a given probability distribution function may prove to be ergonomically optimal or not. It is clear that the scenario presented in figure 3a, while demonstrating the most striking effects of social facilitation, is highly unlike (if not impossible) to exist in nature.
Discussion
No food, water or fresh air supply was available to the confined Nasutitermes workers. Since cannibalism in termites could provide food supply in stressed colonies (Cook & Scott 1933), larger groups could be thought to be subject to less starvation levels per individual than smaller ones, since more prospective food (in the form of nestmates) was available. However, microscope observations of dead individuals did not reveal any sign of cannibalism. Another possible source of food, trophallaxis, is also not important in this context, since it is known to decrease with increasing group size (Afzal, 1983). Therefore, we can assume that all experimental units were reasonably submitted to similar levels of starvation, having theoretically the same average longevity due to food scarcity only.
Interestingly, when other authors have found larger groups to profit from social interactions, it seems that the presence of food in the experiments denoted an assumption that survival would result from the well known increased food intake promoted by social facilitation. Our results, however show that social interactions may enhance survival independently of resource supply. Moreover, such an enhancement might be so strong that it compensates for certain kinds of stresses, as explained below.
Since all tubes were kept hermetically sealed throughout the experiment, larger groups were submitted to stronger pressure due to lack of oxygen. The tendency then would have been to expect workers in larger groups to die at higher rates than those in smaller groups. However, the observed trend was the opposite suggesting that survival is highly correlated with the presence of colony fellows.
The biological mechanisms underlying social facilitation have been revised by Zajonc (1965) (see also Clayton, 1978 for a critical view), who discussed some evidences on changes of activity of endocrine systems related to the mere presence of conspecifics, in humans, monkeys, and mice. It seems reasonable to assume that this could be the mechanism through which the larger groups of termites lived longer. An indirect evidence of this is the reduction of trophallaxis as group size increases (Afzal, 1983). It seems that termites in larger groups are less demanding on food, which supports the idea of metabolic efficiency increasing with group size. That is, social facilitation may trigger increased activity of endocrine systems in such a way that metabolism becomes more efficient, so starving individuals can make better use of body reserves and survive longer. While there are is no conclusive evidence that this is the general case in termites, other studies provide good evidence that individual metabolic rates in ants decrease when individuals are in larger groups (Peakin & Josens, 1978). Nash and Pierce (1994) showed that Iridomyrmex single ants consumed an average volume of 0.0063 ml of oxygen per hour, while grouped ants consumed 0.00168 ml/hr.
To test such an idea, we constructed a model whose only biological parameters are the capacity of interaction with neighbouring individuals and the inevitable death after some time period (see Materials and methods). The results of these simulations are shown in figures 3 and 4 and it is possible to observe that while the specific numerical values for the longevity are different than for groups with no inter-individual variability, the pattern is essentially the same: survival increases as a function of group size. Moreover, the important result to remark is that the dependence between longevity and group size is non-linear. In summary, a synergetic phenomenon arises where the basic generating mechanism is facilitation through individual interactions.
Acknowledgements
We would like to thank M.P. Hassell, M. Crawley, E.Vilela, K. Schönrogge, D. Nash, P. Rohani, M. Bonsall, R. Constanti and A. Chopps for their help, comments and suggestions. O.M. is grateful to the members of the Departamento de Biologia Animal, Universidade Federal de Viçosa for their hospitality during a research visit. This work was partially supported by grants from the Universidad Nacional Autónoma de México and ORS (O.M.).
References
Afzal, M. (1983). Radioisotope studies of trophallaxis in the drywood termite Bifiditermes beesoni (Gardner) (Isoptera). I: effect of group size on the rate of food exchange. Material und Organismen 18, 51-63.
Chauvin, R. (1944). L'effet de groupe et la regulation de l'activité sociale chez les Fourmis du genre Leptothorax. Bull. Biol. Fr. et Belg. 78, 197-205.
Chauvin R., Lafarge J.P. & Saligot, J.P. (1985) L`intervetion d`une hormone, la survivone, dans la mortalité des abeilles (Apis mellifica L.) isolées (effet de groupe). Apidologie 16, 77-88.
Chen, S.C. (1937). Social modification of the activity of ants in nest-building. Physiol. Zool. 10, 420-436.
Clayton, D.A. (1978). Socially facilitated behavior. The Quarterly Review of Biology 53, 373-392.
Cole, B.C. (1992). Short-term activity cycles in ants: age-related changes in tempo and colony synchrony. Behav. Ecol. Sociobiol. 31, 181-187.
Cook, S.F. & Scott, K.G. (1933). The nutritional requirements of Zootermopsis (Termopsis) angusticollis. J. of Cellular Comp. Phys. 4, 95-110.
Crawley, M.J. (1993). GLIM for ecologists. Oxford: Blackwell Scientific Publications.
El Bakary, Z. & Fuzeau-Braesch, S. (1987) Mise en évidence d'un effet du groupement sur la survie des pullus du Scorpion. C.R. Soc. Biol. 181, 502-505.
Fowler, H.G. (1992) Social facilitation during foraging in Agelaia (Hymenoptera: Vespidae) Naturwissenschaften 79, 424.
Grassé, P.P. (1946). Sociétés animales et effet de groupe. Experientia 2, 77-82.
Grassé, P.P. (1986). Termitologia. v.3. Paris: Masson. p.715.
Grassé, P.P. & Chauvin, R. (1944). L'effet de groupe et la survie des neutres dans les sociétés d'insectes. Rev.Sci. 82, 461-464.
Hölldobler B. & Wilson, E.O. (1991). The ants. Berlin: Springer-Verlag.
Hosey, G.R., Wood, M., Thompson, R.J. & Druck, P.L. (1985). Social facilitation in a "non-social" animal, The centipede Lithobius forficatus. Behavioural Processes 10, 123-130.
Klotz, J.H. (1986). Social facilitation among digging ants (Formica subericea). J. of Kansas Entomol. Soc. 59(3), 537-541.
Krishna, K. & Weesner, F.M. (eds), (1970). Biology of termites. New York: Academic Press.
Kurta, A. (1982). Social facilitation of foraging behavior by the Hermit crab, Coenobita compressus, in Costa Rica. Biotropica 14(2), 410.
Lamon, B. & Topoff, H. (1985). Social facilitation of eclosion in the fire ant, Selenopsis Invicta. Developmental Psychobiology 18(5), 367-374.
Lenz, M. & Williams, E.R. (1980). Influence of container, matrix volume and group size on survival and feeding activity in species of Coptotermes and Nasutitermes (Isoptera: Rhinotermitidae, Termitidae). Material und Organismen 15, 25-46.
Miramontes, O., Solé, R. & Goodwin, B.C. (1993a). Collective behaviour of random-activated mobile cellular automata. Physica D 63, 145-160.
Miramontes, O., Solé, R. & Goodwin, B.C. (1993b). Antichaos in ants: the excitability metaphor at two levels. In: Proceedings of the Second European Conference on Artificial Life, 790-807 (Brussels, May 1993).
Müller, C.B. & Schmid-Hempel, R. (1992). To die for host or parasitoid. Anim. Behav. 44, 177-179.
Nash, D.R. & Pierce, N.E. (1994). Cost-benefit analysis of a mutualistm: energetic costs to ants of tending lycaenids. Preprint.
Okot-Kotber, B.M. (1983). Influence of group size and composition on soldier differentiation in female final larval instars of a higher termite Macrotermes michaelseni. Physiological Entomology 8, 41-47.
Oster, G.F. & Wilson, E.O. (1978). Caste and ecology in the social insects. Princeton: Princeton University Press.
Parrish, M.D. & Fowler, H.G. (1983). Contrasting foraging related behaviors in 2 sympatric wasps (Vespula maculifrons and Vespula germanica), Ecol. Entomol. 8: 185.
Peakin, G.J. & Josens, G. (1978). Respiration and energy flow. In: Production Ecology of ants and termites, Brian, M.V. (ed). Cambridge: Cambridge University Press, pp. 111-164.
Pinder III, J.E., Wiener, J.G. & Smith, M.H. (1978). The Weibull distribution: a new method of summarizing survivorship data. Ecology 59: 175-179.
Poulin, R. (1992). Altered behaviour in parasitised bumblebees: Parasite manipulation or adaptive suicide?. Anim. Behav. 44,174-177.
Salzemann, A. & Plateux, L. (1988). Sur le mecanisme de l'effet de groupe stimulant la ponte des ouvrieres de la fourmi Leptothorax nylanderi. Annales des Sciences Naturelles, Zoologie 9, 37-43.
Solé, R., Miramontes, O. & Goodwin, B.C. (1993a). Oscillations and chaos in ant societies. J. Theor. Biol. 161: 343-357.
Solé, R., Miramontes, O. & Goodwin, B.C. (1993b). In: Interdisciplinary Approaches to Non Linear Complex Systems. Haken, H. & Mikhailov, A. (eds). Berlin: Springer-Verlag series on Synergetics.
Springhetti, A. (1990). Nest digging of Kalotermes flavicollis (Fabr.) (Isoptera Kalotermitidae) by groups of different number of pseudergates. Ethology Ecology & Evolution 2, 165-173.
Williams, R.M.C., Perez-Morales, J.V. & Jaisson. P. (1980). The effect of group size on the survival and feeding economy of pseudoworkers of building damaging Cryptotermes spp. (Isoptera, Kalotermitidae). Social insects in the tropics: Proceedings of the first international symposium organized by the International Union for the Study of Social Insects and the Sociedad Mexicana de Entomología. México, pp. 219-234.
Wilson, E.O. (1980). Sociobiology. (The abridged edition). Harvard: Belknap Press.
Zajonc,R.B. (1965) Social facilitation. Science 149, 271-274