A_b can be extracted from A_FB^(0,b) when A_e = 0.1501 ± 0.0016 is taken from a fit to leptonic asymmetries (using lepton universality). The result, A_b=0.886 ± 0.017, is 2.9 σ below the SM prediction^&dagg, and also 1.5 6sigma; below A_b = 0.925 ± 0.020 obtained from A_LR^FB(b) at SLD. Thus it appears that at least some of the problem in A_FB^(0,b) is experimental. Note, however, that the uncertainty in A_FB^(0,b) is strongly statistics dominated. The combined value, A_b= 0.902 ± 0.013 deviates by 2.5 &sigma. It would be extremely difficult to account for this 3.5% deviation by new physics radiative corrections since an order of 20% correction to would be necessary to account for the central value of A_b. If this deviation is due to new physics, it is most likely of free-level type affecting preferentially the third generation. Examples include the decay of a scalar neutrino resonance [142], mixing of the b quark with heavy exotics [143], and a heavy Z' with family-nonuniversal couplings [144]. It is difficult, however, to simultaneously account for R^b, which has been measured on the Z peak and off-peak [145] at LEP 1. An average of R^b measurements at LEP 2 at energies between 133 and 207 GeV is 2.1 σ below the SM prediction, while A_FB^(b)(LEP 2) is 1.6 σ low.

The left-right asymmetry, A_LR⁰= 0.15138 ± 0.00216 [101], based on all hadronic data from 1992-1998 differs 1.9 σ from the SM expectation of 0.1472 ± 0.0011. The combined value of A_l = 0.1513 ± 0.0021 from SLD (using lepton-family universality and including correlations) is also 1.9 σ above the SM prediction; but there is now experimental agreement between this SLD value and the LEP value A_l = 0.1481 ± 0.0027, obtained from a fit to A_FB^(0,l), A_e(P_τ), and A_τ(P_τ), again assuming universality.

Despite these discrepancies the goodness of the fit to all data is excellent with a χ² / d.o.f. = 45.5 / 45. The probability of a larger χ² is 45%. The observables in Table 10.4, as well as some other less precise observables are used in the global fits described below. The correlations on the LEP lineshape and τ polarization, the LEP/SLD heavy flavor observables, the SLD lepton asymmetries, the deep inelastic and ν - e scattering observables, and the m_t measurements, are included. The theoretical correlations between Δα_had⁽⁵⁾ and g_μ - 2, and between the charm and bottom quark masses, are also accounted for.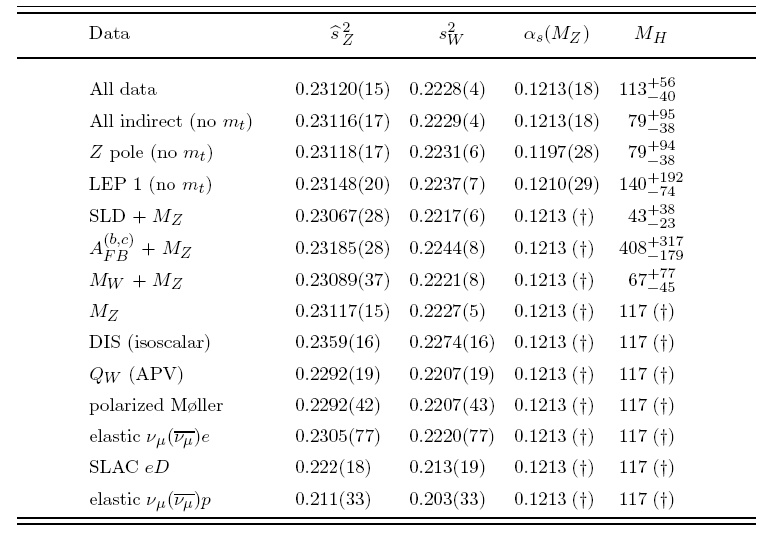

Table 10.2: values of s_Z², s_W², α_s, and M_H in GeV for various (combinations of) observables. Unless indicated otherwise, the top quark mass, m_t = 177.9 ± 4.4 GeV, is used as an additional constraint in the fits. The (†) symbol indicates a fixed parameter.

The data allow a simultaneous determination of M_H, m_t, sin²θ_W, and the strong coupling α_s(M_Z). (m_c, m_t, and Δα_had⁽⁵⁾ are also allowed to float in the fits, subject to the theoretical constraints [5,18] described in Sec. 10.1- Sec. 10.2. These are correlated with α_s).α_s is determined mainly from R_l, Γ_Z, σ_had, and &tau_&tau and is only weakly correlated with the other variables (except for a 10% correlation with m_c). The global fit to all data, including the CDF/D0 average, m_t = 177.9 ± 4.4 GeV, yields

In the on-shell scheme one has s_W² = 0.22280 ± 0.00035, the larger error due to the stronger sensitivity to m_t while the corresponding effective angle is related by Eq. (10.34), i.e.,s_l² = 0.23149 ± 0.00015. The m_t pole mass correspond to m_t(m_t)= 166.8 ± 3.8 GeV. In all fits, the errors include full statistics, systematic, and theoretical uncertaities. The s_Z²(s_l²) error reflects the error on s_f² = 0.23150 ± 0.00016 from a fit to the Z-pole asymmetries.

The weak mixinf angle can be determined from Z-pole observables, M_W, and from a variety of neutral-current processes spanning a very wide Q² range. The results (for the older low-energy neutral-current data see [42,43]) shown in table 10.5 are in reasonable agreement with each other, indicating the quantitative succes of the SM. The largest discrepancy is the values_Z² = 0.2358 ± 0.0016 from DIS which is 2.9 σ above the value 0.23120 ± 0.00015 from the global fit to all data. Similarly, s_Z² = 0.23185 ± 0.00028 from the forward-backward asymmetries into bottom and charm quarks, and s_Z² = 0.23067 ± 0.00028 from the SLD asymmetries (both when combined with M_Z) are 2.3 σ high and 1.9 σ low, respectively.

The extracted Z-pole value of α_s(M_Z) is based on a formula with negligible theoretical uncertainty (± 0.0005 in α_s(M_Z)) if mone assumes the exact validity of the SM. One should keep in mind, however, that this value, α_s = 0.1197 ± 0.0028, is very sensitive to such types of new physics as nonuniversal vertex corrections. In contrast, the value derived from τ decays, α_s(M_Z) = 0.1221_-0.0023^+0.0026[5], is theory dominated but less sensitive to new physics. The fromer is mainly due to the larger value of of α_s(m_τ), but just as the hadronic Z-width the τ lifetime is fully inclusive and can be computed reliably within the operator product expansion. The two values are in excellent agreement with each other. They are also perfect agreement with other recent values, such as 0.1202 ± 0.0049 from jet-events shapes at LEP [146], and 0.121 ± 0.003 [147] from the most recent lattice calculation of the spectrum. For more details and other determinations, see our Section 9 on "Quantum Chromodynamics" in this review.

The data indicate a preference for a small Higgs mass. There is a strong correlation between the quadratic m_t and logarithmic M_H terms in ρ in all of the indirect data except for the Z → bb vertex. Therefore, observables (other than R_b) which favor m_t values hifher than the Tevatron range favor lower values of M_H. This effect is enhanced by R_b, which has little direct M_H dependence but favors the lower end of the Tevatron m_t range. M_W has additional M_H dependence trough Δr_W which is not coupled to m_t² effects. The strongest individual pulls toward smaller M_H are from M_W and A_FB^(0b) and the NuTev results favor high values. The difference in χ² for the global fit is Δχ² = &chi² (M_H = 1000 GeV) - &chi_min²=34.6. hence, the data favor a small value value of M_H, as in supersymmetric extensions of the SM. The central value of the global fit result, M_H = 113_-40⁺⁵⁶ GeV, is slightly below the direct lower bound, M_H ≥ 114.4 GeV (95% CL) [106].

The 90% central confidence range from all precision data is

One can also carry out a fit to the indirect data alone, i.e., without including the constraint, m_t = 177.9 ± 4.4 GeV, obtained by CDF and D0. (The indirect prediction is for the MS mass, m_t(m_t) = 162.5_-6.9^+9.2 GeV, which is in the end converted to the pole mass). One obtains m_t = 174.4_-7.3^+9.8 GeV, with little change in the sin² θ_W and α_s values, in remarkable agreement with the direct CDF/D0 average. The relations between M_H and m_t for various observables are shown in Fig. 10.1.

Using α(M_Z) and s_Z² as inputs, one can predict α(M_Z) assuming grand unification. One predicts [149] α(M_Z) = 0.130 ± 0.001 ± 0.01 for the simplest theories based on the minimal supersymmetric extension of the SM, where the first (second) uncertainty is from the inputs (thresholds). this is slightly larger, but consistent with the experimental α(M_Z) = 0.1213 ± 0.0018 from the Z lineshape and the τ lifetime, as well as with other determinations. Non-supersymmetric unified theories predict the low value α(M_Z) = 0.073 ± 0.001 ± 0.001. See also the note on "Low-Energy Supersymmetry" in the Particle Listings.

One can also determined the radiative correction parameters Δr from the global fit one obtains Δr = 0.0347 ± 0.0011 and Δr_W = 0.06981 ± 0.00032. M_W measurements [41,141] (when combined with M_Z) are equivalent to measurements of Δr = 0.0326 ± 0.0021 which is 1.2 σ below the result from all indirect data, Δr = 0.0355 ± 0.0013. Fig. 10.2 shows the 1 σ contours in the M_W - m_t plane from the direct and indirect determinations, as well as the combined 90% CL region. The indirect determination uses M_Z from LEP 1 as input, which is defined assuming an s-dependent decay width. M_W then correspond to the s-dependent width definition, as well, and can be directly compared with the results from the Tevatron and LEP 2 which have been obtained using the same definition. The difference to a constant width definition is formally only of O(α²), but is strongly enhanced since the decay channels add up coherently. It is about 34 MeV for M_Z and 27 MeV for M_W. The residual difference between working consistently with one or the other definition is about 3 MeV, i.e., of typical size for non-enhanced O(α²) corrections [54,55].

Most of the parameters relevant to ν-hadron, ν-e. e - hadron, and e^- e^{+ processes are determined uniquely and precisely from the data in model independet fits (i.e., fits which allow for an arbitrary electroweak gauge theory). The values for the parameters defined in Eqns. (10.11)-(10.13) are given in table 10.6 along with predictions of the SM. The agreement is reasonable, except for the values of g_L2 and (u,d), which reflect the discrepancy in the recent NuTeV results. (The &nu-hadron results without the new NuTeV data can be found in the previous editions of this Review). The off Z-pole e+ e- results are difficult to present in a model-independent way because Z propagator effects are non-negligible at TRISTAN, PETRA, PEP, and LEP 2 enrgies. However, assuming e - μ - τ universality, the low energy lepton asymmetries imply [98] 4 (g_Ae)2 = 0.99 ± 0.05, in good agreement with the SM prediction ≈ 1.}